A*算法 | Lua版本
A*算法思路
- 从起点A开始, 把它作为待处理的方格存入一个"开启列表", 开启列表就是一个等待检查方格的列表.
- 寻找起点A周围可以到达的方格, 将它们放入"开启列表", 并设置它们的"父方格"为A.
- 从"开启列表"中删除起点 A, 并将起点 A 加入"关闭列表", “关闭列表"中存放的都是不需要再次检查的方格
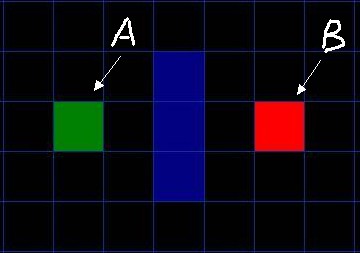
- 从 “开启列表” 中选择 F 值最低的方格 C (绿色起始方块 A 右边的方块), 把它从 “开启列表” 中删除, 并放到 “关闭列表” 中.
- 检查它所有相邻并且可以到达 (障碍物和 “关闭列表” 的方格都不考虑) 的方格. 如果这些方格还不在 “开启列表” 里的话, 将它们加入 “开启列表”, 计算这些方格的 G, H 和 F 值各是多少, 并设置它们的 “父方格” 为 C.
- 如果某个相邻方格 D 已经在 “开启列表” 里了, 检查如果用新的路径 (就是经过C 的路径) 到达它的话, G值是否会更低一些, 如果新的G值更低, 那就把它的 “父方格” 改为目前选中的方格 C, 然后重新计算它的 F 值和 G 值 (H 值不需要重新计算, 因为对于每个方块, H 值是不变的). 如果新的 G 值比较高, 就说明经过 C 再到达 D 不是一个明智的选择, 因为它需要更远的路, 这时我们什么也不做.
- 当我们发现 “开始列表” 里出现了目标终点方块的时候, 说明路径已经被找到.
对每个格子怎么走,往哪个方向走有一个很重要的函数-估价函数, 公式如下:
f(n) = g(n) + h(n)
- g(n) 是指从起始格子到格子n的实际代价。
- h(n) 是指从格子n到终点的的估计代价。
lua代码
astart.lua代码如下
lua
#! /usr/local/bin/lua
--参考: https://blog.csdn.net/u012234115/article/details/47152137
local kCost1=10; --直移一格消耗
local kCost2=14; --移一格消耗
local openList = {}
local closeList = {}
--初始化地图,用二维矩阵代表地图,1表示障碍物,0表示可通
local maze = {
{1,1,1,1,1,1,1,1,1,1,1,1},
{1,0,0,1,1,0,1,0,0,0,0,1},
{1,0,0,1,1,0,0,0,0,0,0,1},
{1,0,0,0,0,0,1,0,0,1,1,1},
{1,1,1,0,0,0,0,0,1,1,0,1},
{1,1,0,1,0,0,0,0,0,0,0,1},
{1,0,1,0,0,0,0,1,0,0,0,1},
{1,1,1,1,1,1,1,1,1,1,1,1}
}
-- F=G+H
--G 表示从起点 A 移动到网格上指定方格的移动耗费 (可沿斜方向移动).
--H 表示从指定的方格移动到终点 B 的预计耗费 (H 有很多计算方法, 本文代码使用简单的欧几里得距离计算方法).
local function calcG(startP, point)
local extraG = math.abs(point.x-startP.x)+math.abs(point.y-startP.y)==1 and kCost1 or kCost2
local parentG = (next(point.parent or {})) and point.parent.G or 0
return parentG + extraG
end
local function calcH(point, endP)
--用简单的欧几里得距离计算H,这个H的计算是关键,还有很多算法
return math.sqrt((endP.x-point.x)^2 + (endP.y-point.y)^2)
end
local function calcF(point)
return point.G + point.H
end
local function getPointString(point)
return "<"..point.x.. ","..point.y..">"
end
local function isInList(tbl, target)
for _,v in ipairs(tbl) do
if target.x == v.x and target.y == v.y then
return v
end
end
return nil
end
--判断某点是否可以用于下一步判断
local function isCanreach(point, target, ignore)
--如果目标点超出地图、与当前节点重合、是障碍物、或者在关闭列表中,返回false
if target.x<1 or target.x>#maze
or target.y<1 or target.y>#maze[1]
or maze[target.x][target.y]==1
or (target.x==point.x and target.y==point.y) then return false end
if isInList(closeList, target) then
--print("target in closeList: ".. getPointString(target))
return false
end
--非斜角可以
if math.abs(point.x-target.x) + math.abs(point.y-target.y) == 1 then return true end
--斜对角要判断是否绊住
if maze[point.x][target.y] == 0 and maze[target.x][point.y] == 0 then return true end
return ignore
end
--获取节点周围的节点
local function getSurroundP(point, ignore)
local surroundP = {}
for i=point.x-1, point.x+1 do
for j=point.y-1, point.y+1 do
local tmp = {x=i,y=j, G=0, H=0, F=0}
if isCanreach(point, tmp, ignore)then
table.insert(surroundP, tmp)
else
--print("not search: point:" .. getPointString(point) .. "; target: ".. getPointString(tmp))
end
end
end
return surroundP
end
local function getLeastFPoint()
local cur = 1
local curP = openList[1]
if not curP then return end
for i, v in ipairs(openList) do
if v.F < curP.F then
curP = v
cur = i
end
end
return cur,curP
end
local function findPath(startP, endP, ignore)
table.insert(openList, startP) --置入起点
while next(openList) do
local cur, curP = getLeastFPoint()--找到最小的F
table.remove(openList, cur) --从开启列表中删除
table.insert(closeList, curP) --放到关闭列表
--1.找到当前周围八个格中可以通过的格子
local surroundP = getSurroundP(curP, ignore)
--print("curP: " .. getPointString(curP).." ####surroundP: "..#surroundP)
for _, target in ipairs(surroundP) do
--2,对某一个格子,如果它不在开启列表中,加入到开启列表,设置当前格为其父节点,计算F G H
if not isInList(openList, target) then
target.parent = curP
target.G = calcG(curP, target)
target.H = calcH(target, endP)
target.F = calcF(target)
table.insert(openList, target)
else
--3,对某一个格子,它在开启列表中,计算G值, 如果比原来的大, 就什么都不做, 否则设置它的父节点为当前点,并更新G和F
local tempG = calcG(curP, target)
if tempG < target.G then
target.parent = curP
target.G = tempG
target.F = calcF(target)
end
end
for i, v in ipairs(openList) do
--print("openList: " .. getPointString(v))
end
local resP = isInList(openList, endP)
if resP then
return resP
end
end
end
return nil
end
local function GetPath(startP, endP, ignore)
local result = findPath(startP, endP, ignore)
local path = {}
while result do
table.insert(path, 1, result)
result = result.parent
end
openList = {}
closeList = {}
return path
end
print("start findPath.....")
local startP = {x=2, y=2, G=0,H=0,F=0}
local endP = {x=7, y=11, G=0,H=0,F=0}
local path = GetPath(startP, endP, false)
for _, v in ipairs(path) do
print(getPointString(v))
end
print("end.....")
执行:
shell
$ lua astart.lua
start .....
<2,2>
<3,2>
<4,3>
<4,4>
<4,5>
<5,6>
<5,7>
<6,8>
<6,9>
<6,10>
<7,11>
end.....
参考连接:https://blog.csdn.net/u012234115/article/details/47152137
--完--
- 原文作者: 留白
- 原文链接: https://zfunnily.github.io/2021/12/astar/
- 更新时间:2024-04-16 01:01:05
- 本文声明:转载请标记原文作者及链接